Selon une légende très ancienne, il existe un temple où les moines sont chargés de veiller sur 64 disques sacrés. Les disques, qui sont tous de taille différente, forment une tour. Comme ils sont précieux et très fragiles, un disque ne peut être placé sur un disque plus petit. Hélas, le jour vient où quelques travaux dans le temple sont nécessaires et les disques doivent être déplacés. Ils sont très lourds et ne peuvent donc être transportés qu’un par un. De plus, il n’y a qu’un seul endroit assez sacré pour les stocker. Les moines commencent donc à déplacer les disques de la tour d’origine vers la nouvelle place et l’endroit intermédiaire, gardant toujours chacune des trois piles en ordre (le disque le plus large en bas, le moins large en haut). Alors qu’ils travaillent, les moines gardent en tête la terrible prophétie : « Le temple s’écroulera avant que les disques soient mis en place. »
Origine du nom
Le problème mathématique des tours de Hanoï a été inventé par Êdouard Lucas en 1883. Il le publia sous le pseudonyme de N. Claus de Siam soi-disant professeur au collège de Li-Sou-Stian (une double anagramme de Lucas d’Amiens, sa ville de naissance, et Saint Louis, le lycée où Lucas enseignait).
Selon l’auteur, le problème serait originaire d’Inde où une légende raconte que dans un temple où se trouvent trois poteaux sur lesquels s’empilent 64 disques d’or, les prêtres de Brahmâ déplacent continuellement les disques selon les règles édictées ci-dessus. D’après cette même légende, le dernier déplacement de disque marquera la fin du monde. Cette légende existe sous plusieurs versions et dans différentes religions.

Comme indiqué ci-dessous, un jeu à 64 disques requiert un minimum de 264-1 déplacements au minimum, soit plus de 40 fois le nombre de secondes écoulées depuis l’origine de l’Univers. La référence à Hanoï, capitale du Viêt Nam, provient sans doute du fait que, dans cette ancienne colonie française de tradition bouddhiste, on retrouve beaucoup de pagodes dont la forme évoque l’empilement des disques de ce problème.
Nombre de déplacements à effectuer
Il est facile de démontrer par récurrence que si N est le nombre de disques, il faut 2N – 1 coups au minimum pour parvenir à ses fins, ce qui augmente très rapidement le temps nécessaire pour résoudre ce problème. En effet, soient a, b et c les trois emplacements des tours. Notons xN le nombre de déplacements de disques nécessaires au déplacement d’une tour complète. Pour déplacer une tour de N disques de a vers c, on déplace la tour des N-1 premiers disques de a vers b, puis le disque N de a vers c, puis la tour des N-1 disques de b vers c. Le nombre de déplacements de disques vérifie donc la relation de récurrence :
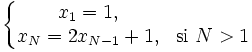
Quelques liens pour jouer en ligne :
http://perso.orange.fr/jeux.lulu/html/hanoi/hanoi1.htm
www.crocodilus.org/jeux/tours/hanoi.htm
